本文使用 Zhihu On VSCode 创作并发布

• 关键词：Jaya；NEORL; 并行计算

Jaya算法由Rao于2016年发表于 International Journal of Industrial Engineering Computations 。

该算法最大的特点是除种群数外无需设置自身参数! 因此十分容易实现。

先从Jaya算法的流程图来理解算法的原理：

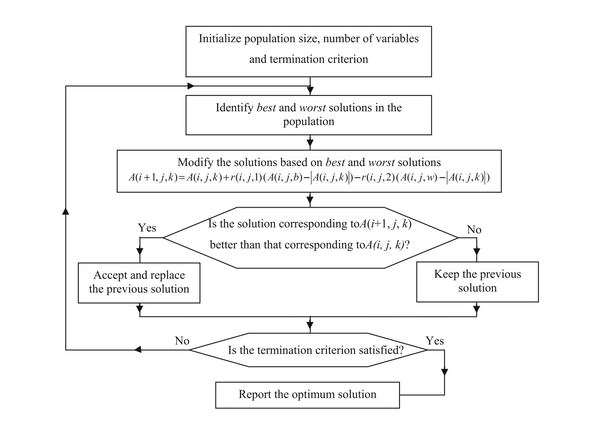
1. 首先初始化种群个体数量，确定每个个体长度以及终止判据
2. 找到当前种群下的最优个体 best 和最差个体 worst
3. 遍历所有个体，根据公式(1)更新个体参数
4. 判断更新后的个体是否优于更新前的个体，若是，则更新个体，否则保留原个体到下一代
5. 判断当前最优个体是否满足终止判据，若是则结束程序，否则遍历步骤2-4

• 其中，i，j，k分别代表迭代代数，个体的某变量，种群中某个体
  • 例如， 表示迭代第i轮时，种群中第k个个体的第j个变量；
• 和分别代表i代时种群中的最优个体和最差个体的第j个变量；
• 和分别控制缩放大小,取值在[0,1]之间；
• 该公式是Jaya算法的核心，后续会从更加直观的角度来解释这个公式

我们用如下二维空间示意图来展示迭代过程中个体一个参数的更新：

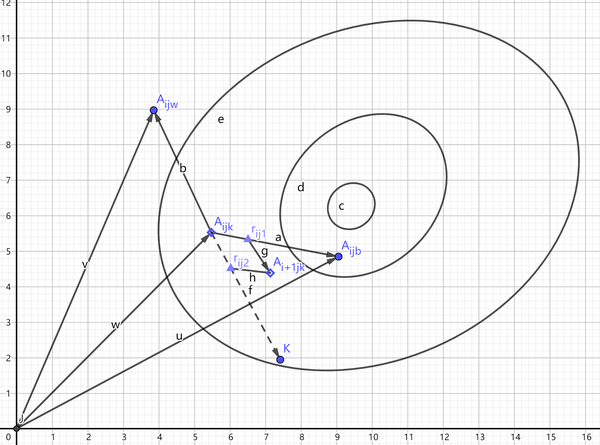
其中，, 分别代表当前迭代轮次下最差个体和最优个体第j个参数的值，是待计算的个体。

公式中在图中就是由指向的向量，而则表示取向量多少长度；

同样的在图中就是由指向的向量，而则表示取向量多少长度,注意公式中前面带了个负号，因此该方向要取反；

最终，公式由, , 三部分相加，更新后的距离最优点更近了。不断重复上述操作，从而逼近最优解，取得胜利（在梵语中，（jaya）意思是“胜利”）

Jaya更新过程中感觉像是一个"趋利避害"的过程，当前的个体会不断向目前最优解靠近，并且远离最差解。

我们仍然以五维球形函数的最优化计算为例子，展示如何用Jaya寻找其最优解

from neorl import JAYA

#Define the fitness function
def FIT(individual):
    """Sphere test objective function.
                    F(x)=sum_{i=1}^d xi^2
                    d=1,2,3,...
                    Range:[-100,100]
                    Minima: 0
    """
    y=sum(x**2 for x in individual)
    return y

#Setup the parameter space (d=5)
nx=5
BOUNDS={}
for i in range(1,nx+1):
    BOUNDS['x'+str(i)]=['float', -100, 100]

#setup and evolute JAYA 
jaya=JAYA(mode='min', bounds=BOUNDS, fit=FIT, npop=60, ncores=1, seed=1)
x_best, y_best, jaya_hist=jaya.evolute(ngen=200, verbose=1)

计算结果如下，可以看到经过200轮迭代，算法找到的结果在e-13次量级：

------------------------ JAYA Summary ------------------------
Best fitness (y) found: -2.634761856007867e-13
Best individual (x) found: [2.09164940e-07 3.16050179e-07 1.82223957e-08 1.13215622e-07
 3.26632308e-07]
--------------------------------------------------------------

NEORL中该算法的描述：https://neorl.readthedocs.io/en/latest/modules/jaya.html

[1]Rao, R. (2016). Jaya: A simple and new optimization algorithm for solving constrained and unconstrained optimization problems. International Journal of Industrial Engineering Computations, 7(1), 19-34.

[2]https://vlight.me/2018/06/19/Jaya-Optimization-Algorithm-and-Its-Variants/